ENE-28
EL método de las fracciones parciales consiste en reducir un cociente de polinomios en fracciones más simples, que permitan obtener de manera inmediata una integral o una transformada de Laplace Inversa. El requisito más importante es que el grado del polinomio del denominador sea estrictamente mayor que el grado del numerador.
Definimos fracciones parciales a la función F(x)en la cual dicha función depende de un numerador y un denominador. Para que sea una fracción parcial el grado del denominador tiene que ser mayor al grado del numerador.
Una guía para obtener la descomposición en fracciones parciales de P(x)/Q(x)
- Si el grado de P(x)no es menor que el de Q(x)se deben dividir los polinomios para obtener la forma apropiada.
- Expresar Q(x) como un producto de factores lineales aix+ b o formas cuadráticas irreducibles ax2+bx+c y agrupar los factores repetidos para que Q(x) quede expresado por un producto de factores distintos de la forma (ax+b)m o bien (ax2+bx+c)n con m y n enteros no negativos.
Integración por fracciones parciales.
EL método de las fracciones parciales consiste en reducir un cociente de polinomios en fracciones más simples, que permitan obtener de manera inmediata una integral o una transformada de Laplace Inversa. El requisito más importante es que el grado del polinomio del denominador sea estrictamente mayor que el grado del numerador.
Definimos fracciones parciales a la función F(x)en la cual dicha función depende de un numerador y un denominador. Para que sea una fracción parcial el grado del denominador tiene que ser mayor al grado del numerador.
Una guía para obtener la descomposición en fracciones parciales de P(x)/Q(x)
- Si el grado de P(x)no es menor que el de Q(x)se deben dividir los polinomios para obtener la forma apropiada.
- Expresar Q(x) como un producto de factores lineales aix+ b o formas cuadráticas irreducibles ax2+bx+c y agrupar los factores repetidos para que Q(x) quede expresado por un producto de factores distintos de la forma (ax+b)m o bien (ax2+bx+c)n con m y n enteros no negativos.
Ejercicio de repaso
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-
FEB-03
MÉTODOS INTEGRALES DE FRACCIONES PARCIALES Caso 1 y 2
Caso 1: Factores lineales distintos
Caso 2: Factores lineales repetidos
Ejercicio de repaso
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-
FEB-03
MÉTODOS INTEGRALES DE FRACCIONES PARCIALES Caso 3 y 4
Ejercicio de repaso
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-
FEB-10
CONTINUACIÓN DE LA CLASE#17 MÉTODOS INTEGRALES DE FRACCIONES PARCIALES
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-
FEB-11
LECCIÓN #1 II PARCIAL CII 2021-2022
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-
FEB-17
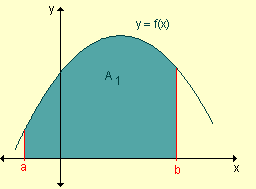
APLICACIÓN DE CI A TRAVÉS DE LA INTEGRAL DEFINIDA EN EL CÁLCULO DE ÁREAS
La Integral Definida de una función se usa para calcular las áreas de recintos planos, los cuales están delimitados por curvas y rectas.
Ejercicio de repaso
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-
FEB-18
CÁLCULO DE ÁREAS EN CURVAS POLARES
Ejercicio de repaso
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-
FEB-24
ÁREAS EN CURVAS POLARES
Ejercicio de repaso
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-
MAR-03
LECCIÓN #2 II PARCIAL CII 2021-2022
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-
MAR-10
LONGUITUD DE UNA CURVALa idea para calcular la longitud de una curva contenida en el plano o en el espacio consiste en dividirla en segmentos pequeños, escogiendo una familia finita de puntos en C, y aproximar la longitud mediante la longitud de la poligonal que pasa por dichos puntos. Cuantos más puntos escojamos en C, mejor sería el valor obtenido como aproximación de la longitud de C.
La idea para calcular la longitud de una curva contenida en el plano o en el espacio consiste en dividirla en segmentos pequeños, escogiendo una familia finita de puntos en C, y aproximar la longitud mediante la longitud de la poligonal que pasa por dichos puntos. Cuantos más puntos escojamos en C, mejor sería el valor obtenido como aproximación de la longitud de C.
Ejercicio de repaso
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-
MAR-11
APLICACIÓN CÁLCULO INTEGRAL EN FÍSICALas integrales definidas son comúnmente usadas para resolver problemas de movimiento, por ejemplo, al razonar sobre la posición de un objeto en movimiento dada cierta información sobre su velocidad. Aprende cómo se hace esto y sobre la diferencia crucial entre velocidad y rapidez.
Los problemas de movimiento son muy comunes en el cálculo. En cálculo diferencial, razonamos sobre la velocidad de un objeto dada su función de posición. En cálculo integral, vamos en la dirección opuesta: dada la función de velocidad de un objeto en movimiento, razonamos sobre su posición o sobre el cambio en su posición.




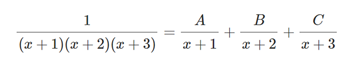





























































No hay comentarios:
Publicar un comentario