UNIDAD #1

DIC-02

CLASE #1 

CÁLCULO DIFERENCIAL Y SU RELACIÓN CON EL CÁLCULO INTEGRAL.

El Cálculo Diferencial estudia la operación denominada diferenciación o derivación y el Cálculo Integral estudia la operación denominada integración. Este importantísimo teorema establece la relación entre dos ramas de las Matemáticas que durante siglos fueron tratadas como independientes, Cálculo Diferencial y Cálculo Integral.

Ejercicio de repaso

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

 

DIC-03

CLASE #2

REGLAS DE LA DERIVACIÓN 

Las reglas de derivación son los métodos que se emplean para calcular la derivada de una función. Son un conjunto de procedimientos que permiten con más facilidad el cálculo de la función derivada sin tener que recurrir a la definición de derivada, que a menuda conlleva cálculos tediosos.

Reglas

1. La derivada de una constante

1. La derivada de una potencia positiva

1. la derivada de una constante por función

1. la derivada de una suma

1. la derivada de un producto

1. La derivada de una cociente.

1. la derivadas de las funciones trigonométricas 

Ejercicio de repaso

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

DIC-09

CLASE #3

INTEGRALES INDEFINIDAS Y DEFINIDAS

La inversa de la integral es diferencial y la inversa de la diferencial es integral. Una integral definida de una función de una variable desconocida es la representación de un número que tiene límites superior e inferior. Una integral indefinida es la representación de una familia de funciones sin límites.

los diferencia entre integral definida e indefinida es que una integral definida se define como la integral que tiene límites superior e inferior y tiene un valor constante como solución, por otro lado, una integral indefinida se define como la interna que no tiene límites aplicados y da una solución general para un problema.

Ejercicio de repaso

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

DIC-10

CLASE #4

INTEGRALES DEFINIDAS

La integral definida es un caso de la integral utilizado para determinar el valor de las áreas delimitadas por una gráfica dentro de un intervalo y el eje horizontal.

Dada una función f(x) de una variable real x y un intervalo [a,b] de la recta real, la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las líneas verticales.

x = a y x = b.

Ejercicio de repaso

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

DIC-16

CLASE #5

LECCIÓN #1 CII 2021 MA2-1

-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

DIC-17

CLASE #6

Resolución de taller 1

En esta clase resolvimos el primer taller enviado el día anterior.

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

DIC-23

CLASE #7

MÉTODO DE INTEGRACIÓN CON CAMBIO DE VARIABLE

El método integración por sustitución o cambio de variable se utiliza para evaluar integrales. El método se basa en realizar de manera adecuada un cambio de variable que permita convertir el integrando en algo sencillo. Este método realiza lo opuesto a la regla de la cadena.

Ejemplos simples de integrales indefinidas

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

ENE-06

CLASE #8

SUMA DE RIEMANN

Es un método para aproximar el área total bajo la gráfica de una curva. Estas sumas toman su nombre del matemático alemán BERNHARD REIMANN.

Es una operación sobre una función continua y limitada en un intervalo [a; b], donde a y b son llamados los extremos de la integración. La operación consiste en hallar el límite de la suma de productos entre el valor de la función en un punto xi* y el ancho Δx del subintervalo conteniendo al punto.

Normalmente se denota con: 

                

La integral de Riemann es una forma simple de definir la integral de una función  sobre un intervalo como el área bajo la curva de la función.

Para obtener una aproximación al área encerrada debajo de una curva, se la puede dividir en rectángulos como indica la figura.

Videos de ayuda

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

ENE-07

CLASE #9

MÉTODO DE INTEGRANCIÓN POR PARTE

Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:.

Regla mnemotécnica: Un Día Vi Una Vaca MENOS Flaca Vestida De Uniforme (UDV = UV - FVDU).

Aunque se trata de un método simple, hay que aplicarlo correctamente.

Método:

1.     El integrando debe ser un producto de dos factores.

2.     Uno de los factores será u y el otro será dv.

3.     Se calcula du derivando u y se calcula v integrando dv.

4.     Se aplica la fórmula.

Ejercicio de repaso

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

ENE-13

CLASE #10

LECCIÓN #2 CII 2021 MA2-1

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

ENE-14

CLASE #11

INTEGRALES DE FUNCIONES TRIGONOMÉTRICAS. 

Una integral se denomina trigonométrica cuando el integrando de la misma está compuesto de funciones trigonométricas y constantes. Para su resolución desde luego que son válidos los teoremas de integración. 

En LO GENERAL SE DEBEN APLICAR LAS SIGUIENTES SUGERENCIAS:

1. USAR UNA IDENTIDAD TRIGONOMÉTRICA Y SIMPLIFICAR, ES ÚTIL CUANDO SE PRESENTAN FUNCIONES TRIGONOMÉTRICAS.

2. ELIMINAR UNA RAÍZ CUADRADA, SE PRESENTA NORMALMENTE DESPUÉS DE COMPLETAR UN CUADRADO O UNA SUSTITUCIÓN TRIGONOMÉTRICA.

3. REDUCIR UNA FRACCIÓN IMPROPIA.

4. SEPARAR LOS ELEMENTOS DEL NUMERADOR DE UNA FRACCIÓN ENTRE EL DENOMINADOR DE LA FRACCIÓN.

5. MULTIPLICAR POR UNA FORMA UNITARIA G(X)/G(X) QUE AL MULTIPLICAR POR EL INTEGRANDO F(X) PERMITA MODIFICAR ADECUADAMENTE [F(X)G(X)]/G(X).

6. PROBAR SUSTITUIR F(X) POR 1/(1/F(X)).

Se aplica el seno y coseno del ángulo mitad:

VIDEO INTEGRALES TRIGONOMÉTRICAS

Ejercicio de repaso

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

ENE-20

CLASE #12

INTEGRALES POR SUSTITUCIÓN TRIGONOMÉTRICA

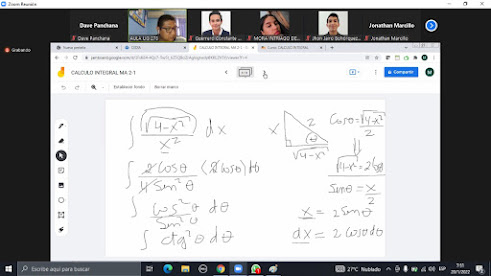
Este método, el cual es un caso especial de cambio de variable, nos permitirá integrar cierto tipo de funciones algebraicas cuyas integrales indefinidas son funciones trigonométricas, las sustituciones que involucran funciones trigonométricas se pueden llevar a cabo en aquellas integrales cuyo integrando contiene una expresión de la forma

La sustitución trigonométrica permite transformar una integral en otra que contiene funciones trigonométricas cuyo proceso de integración es más sencillo.

Este método se basa en el uso de triángulos rectángulos, el teorema de Pitágoras e identidades trigonométricas. ´ Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos: En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados llamamos "triángulo rectángulo" a un triángulo con un ángulo recto.

3´2 + 4´2 = 5´2

Calculando obtenemos:9 + 16 = 25

Ejercicio de repaso

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

ENE-21

CLASE #13

LECCIÓN #2 CII 2021 MA2-1

_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-

ENE-27

CLASE #14

EXAMEN I PARCIAL CIINTEGRAL MA 2-1 CII 2021 - 2022